Large earthquakes follow ‘Devil’s Staircase’ mathematical pattern

According to a new study published in the Bulletin of the Seismological Society of America, the occurrence of large shallow earthquakes worldwide follows a mathematical pattern called the Devil's Staircase, wherein clusters of seismic events are separated by long but irregular intervals of seismic quiet. The result in this study is different from the pattern predicted by classical models.

The Devil's Staircase pattern, sometimes called a Cantor function, is a fractal demonstrated by nonlinear dynamic systems, wherein a change in any portion could impact the behavior of the whole system. In nature, the pattern can be seen in sedimentation sequences, changes in uplift and erosion rates and reversal in the magnetic field of the Earth, for instance.

This pattern is evident in huge earthquakes in the Great Basin, spanning Nevada, most of Oregon and Utah, and portions of California, Idaho, and Wyoming.

The same pattern is also found in Australia, on the Africa-Eurasia plate boundary off western Algeria coast, along the Dead Sea Transform Fault, and likely in the New Madrid seismic zone of central U.S., according to researcher Dr. Mian Liu.

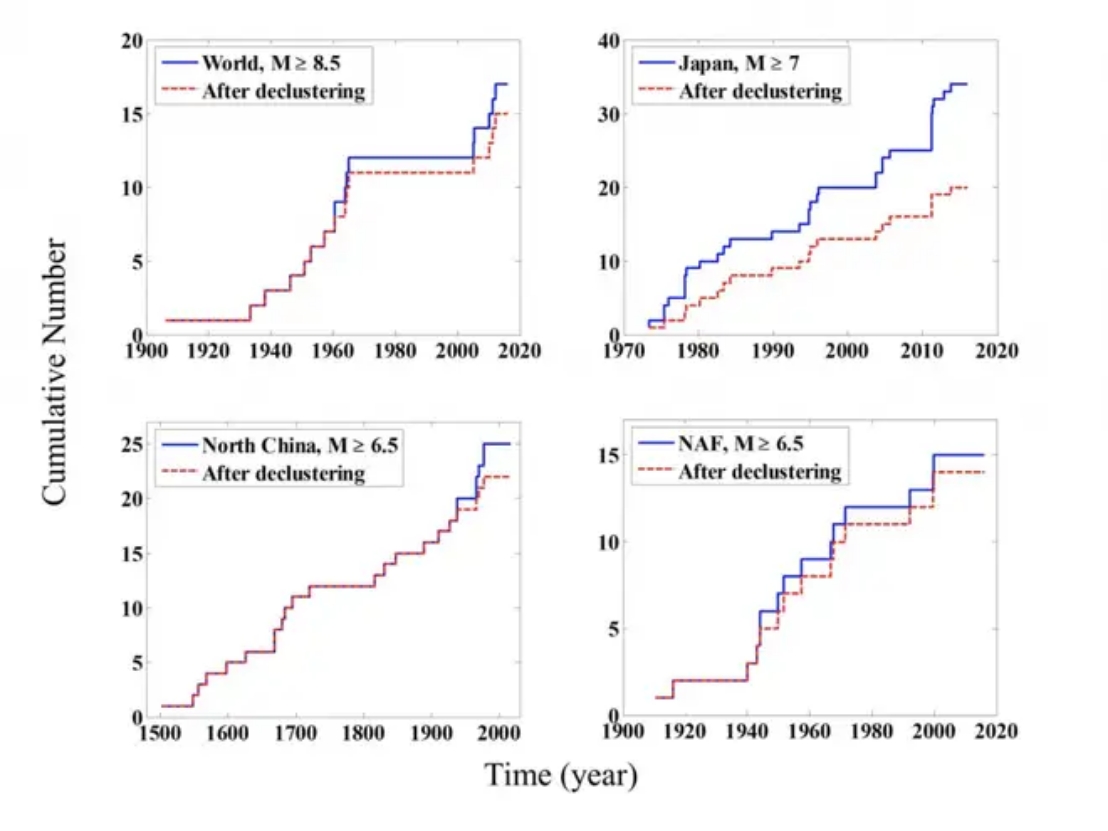
Image credit: Bulletin of the Seismological Society of America

The result in this study is different from the pattern predicted by classical models that suggest cycles of build-up and release of tectonic stress would make tremors occur periodically.

Yuxuan Chen, the study's lead author, said periodic large earthquake sequences are relatively unusual. Liu, also Chen's Ph.D. supervisor, learned of the Devil's Staircase pattern in an unprecedented way– by reading a study of the temporal pattern of a serial killer from the former Soviet Union.

"I stumbled into this topic a few years ago when I read about two UCLA researchers' study of the temporal pattern of a notorious serial killer, Andrei Chikatilo, who killed at least 52 people from 1979 to 1990 in the former Soviet Union," Liu explained.

"The time pattern of his killings is a Devil's staircase. The researchers were trying to understand how the criminal's mind worked, how neurons stimulate each other in the brain. I was intrigued because I realized that earthquakes work in a similar way, that a fault rupture could stimulate activity on other faults by stress transfer."

Liu added, "Conceptually, we also know that many large earthquakes, which involve rupture of multiple and variable fault segments in each rupture, violate the basic assumption of the periodic earthquakes model, which is based on repeated accumulation and release of energy on a given fault plane."

Researcher and co-author Gang Luo of Wuhan University said the factors controlling the clustered events are complex and may involve the stress that triggers an earthquake, changes in frictional properties, and stress transfer between faults or fault segments in the event of a rupture, among other factors. He also remarked that the intervals appear to be inversely related to the background tectonic strain rate for a region.

Reference

"Complex Temporal Patterns of Large Earthquakes: Devil’s Staircases" – Chen, Y. et al. – Bulletin of the Seismological Society of America – DOI: 10.1785/0120190148

Abstract

Periodic or quasiperiodic earthquake recurrence on individual faults, as predicted by the elastic rebound model, is not common in nature. Instead, most earthquake sequences are complex and variable, and often show clusters of events separated by long but irregular intervals of quiescence. Such temporal patterns are especially common for large earthquakes in complex fault zones or regional and global fault networks. Mathematically described as the Devil’s Staircase, such temporal patterns are a fractal property of nonlinear complex systems, in which a change of any part (e.g., rupture of a fault or fault segment) could affect the behavior of the whole system. We found that the lengths of the quiescent intervals between clusters are inversely related to tectonic‐loading rates, whereas earthquake clustering can be attributed to many factors, including earthquake‐induced viscoelastic relaxation and fault interaction. Whereas the underlying causes of the characteristics of earthquake sequences are not fully known, we attempted to statistically characterize these sequences. We found that most earthquake sequences are burstier than the Poisson model commonly used in probabilistic seismic hazard analysis, implying a higher probability of repeating events soon after a large earthquake.

Featured image credit: Mihai Turturica